Figures marked "CSIRO", are copyright CSIRO, but please feel free to use them, conditional on the figures not being altered, and their source being acknowledged, and with a link to this site where possible.

All other figures are copyright. Please do not copy without the owner's permission.

Sea level measurements

Satellite altimeters

A more detailed version of the introductory material here is available at ESA's radar altimeter tutorial.

• Introduction
• Gravity/geoid models
• Satellite altimeter missions
• TOPEX/Poseidon

Introduction

Use of satellite radar altimeters to measure global sea surface height (SSH) has come a long way since the brief Seasat mission of 1978. Early missions measured SSH with an accuracy of tens of metres. More recent high quality satellite altimeter missions such as TOPEX/Poseidon (launched August 1992) and Jason-1 (launched December 2001) measure SSH to an accuracy of a few centimetres. These satellites were specifically designed to measure SSH to the highest possible accuracy.

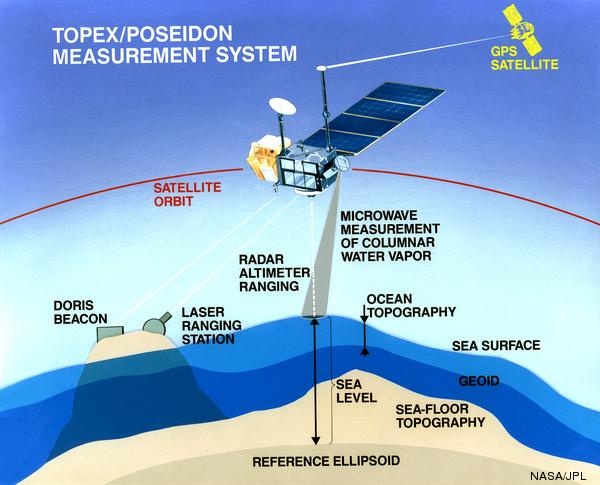
The essential parts of a satellite altimeter measuring system are:

• A satellite in an orbit which repeats the same ground track very closely (within about 1 kilometre)
  
• A radar system to measure the distance from the satellite to the sea surface to high accuracy. TOPEX/Poseidon and Jason-1 use two radar frequencies, Ku band (13.6GHz) and C band (5.3Ghz).
  
• A tracking system capable of locating the satellite vertically at any time to within a few centimetres. Some of the components of such a system are:
• Systems (usually a combination of GPS, SLR (Satellite Laser Ranging) and the French DORIS system) to locate the satellite
• A high quality gravity model
• A model of the drag from solar wind and the atmosphere
• Suitable software to combine all of the above

• Other corrections to correct the range:


• On the satellite:
• A water vapour radiometer to measure the amount of water vapour between the satellite and the sea surface (the water vapour slows down the radar pulse, causing the raw measurement to be too long)
• Measurement of the range at two frequencies to estimate the "ionospheric correction" - that is, the degree to which the radar pulse is slowed down by free electrons in the ionosphere
• The troughs of waves contribute more to the radar reflection than the crests, so we need a corection for this. This is estimated from the wind speed and the wave height, both of which can be estimated from the characteristics of the returned radar pulse.


• On the ground:
• Ocean tide models to convert the raw altimeter measurement to the "detided" SSH
• Estimates (from a model) of the atmospheric pressure. This is used to calculate a correction to the radar range to compensate for the fact that the atmosphere slows down the radar pulse
• A correction is made for the "inverse barometer" effect, where sea level is depressed in areas of high atmospheric pressure, and vice versa
  

The picture below illustrates some of this.

[top]

Gravity/geoid models

The Earth is not spherical and both the gravity field and the (related) geoid (the equipotential surface) vary over the surface of the Earth. Oceanographic signals are small perturbations (typically less than a metre) on the geoid signal (which has a range of about 200 metres). Some early altimeter missions, such as the GEOSAT Geodetic Mission (see table below) were initially put up (by the US Navy) to measure the marine geoid, which then lead to estimates of the marine gravity field (apparently you need to know the exact differene between gravitational vertical and actual vertical to target missiles accurately).

High precision satellite altimetry needs high quality gravity fields to estimate the perturbations in the satellite's orbits caused by the spatial changes in the gravity field. This is at the stage now where the changes in mass (and hence gravity) caused by movement of the oceans by tides need to be included in the gravity models to get the best possible altimeter orbits.

Many Earth-observing satellites are in fairly low (up to about 800 kilometres above the Earth's surface), but TOPEX/Poseidon and Jason-1 used higher (about 1340 kilometres) orbits as this helped with orbit determination because the gravity field is a bit smoother at this higher altitude. Also there is less atmospheric drag on the satellite at this height. The payback for this is that the missions are more expensive because of the higher launch costs and the satellites have to work in a harsher radiation environment as there is less of the Earth's atmosphere to protect them.

[top]

Satellite altimeter missions

Notes on the table:

• Heights are heights above the Earth's surface
• "Inclination" is the angle between the plane of the satellite's orbit and the equator. A satellite going over the poles would have an inclination of 90°
• A satellite in a prograde orbit (e.g. TOPEX/Poseidon) is always moving east relative to the Earth. A satellite in a retrograde orbit (e.g. GFO) is always moving west relative to the Earth
• A sun-synchronous orbit (ERS-1/2, Envisat) is one in which the satellite passes over any location on the Earth at the same local time every cycle.
• The repeat time (or cycle length) is the time between subsequent overpasses of the same point on the Earth's surface.
• TOPEX/Poseidon was moved into a new orbit (same inclination and cycle length, but moved longitudinally) in August, 2002.

[top]

TOPEX/Poseidon

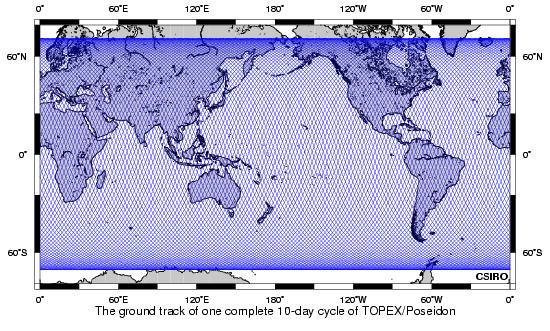
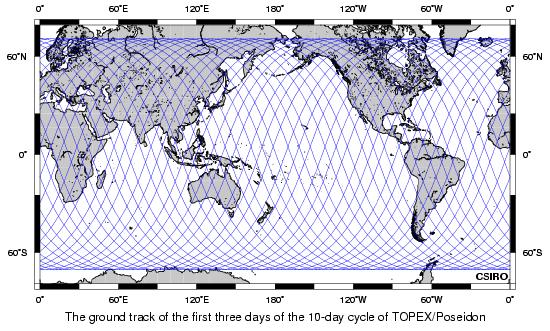
It may be easier to see what is happening from this subset (the first three days) of the the 10-day cycle.

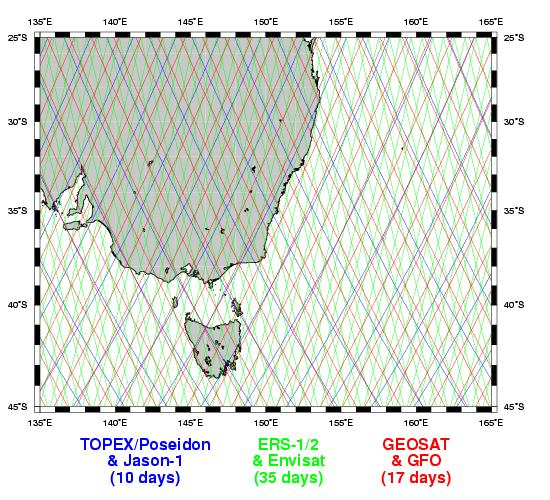
This plot shows the tracks of three different satellites over the south-eastern part of Australia.

 

Some facts about the TOPEX/Poseidon (and Jason-1) orbit

• Each 10-day (actually 9.916 days) cycle consists of 127 revolutions ("orbits"), which can be broken up into 127 ascending and 127 descending half-orbits ("passes"). For a prograde orbit like TOPEX/Poseidon, ascending passes go South-West to North-East, and descending passes go North-West to South-East.
• each complete orbit (full revolution) takes approximately 1 hour and 52 minutes.
• orbit height is about 1,340 kilometres (it varies slightly because of the shape of the Earth, (a slightly pear-shaped, flattened sphere) and the (small) eccentricity of the orbit. For comparison, the radius of the Earth is about 6,370 kilometres.
• The inclination of 66.04° means that the maximum latitude it reaches is 66.04°(N or S). Note that the ground track spans Drake Passage (between the southern tip of South America and Antarctica), one of the major choke points in the oceanic circulation. This was one of the design criteria for this satellite.
• the ground track repeats within ±1 kilometre of the nominal track.
• the orbit was chosen to maximise the potential for solving for the most important ocean tides. Major advances in estimation of tides and understanding of the underlying science have come from this mission.
• Altimeter orbits are usually chosen with as low an eccentricity (i.e. as near-circular) as possible - but it is usually non-zero as this parameter is what is used to "lock" the orbit into an exactly repeating pattern. The TOPEX/Poseidon orbit had an eccentricity of 0.000095.

[top]

Website owner: Benoit Legresy | Last modified 15/02/10

CMAR Home | CSIRO Oceans and Atmosphere | ACE CRC
Legal Notice and Disclaimer | Copyright