

|
|||
"C-squares" (acronym for "concise spatial query and representation system") is a grid based global locator system developed to facilitate the indexing, searching, and retrieval of georeferenced ("spatial") information within an intuitive, human- and machine-readable notation system. The system was developed by Dr Tony Rees of CSIRO Marine and Atmospheric Research in Australia (now CSIRO Marine and Atmospheric Research or CMAR) in 2001-2002 and is freely available for use worldwide without royalty or licence. At its core, the system comprises a hierarchical nomenclature for global grid squares at a resolution of n×n degrees, where n represents a number from the sequence 10, 5, 1, 0.5, 0.1, 0.05, etc., expressed in decimal degrees according to the WGS84 datum. Each resulting square ("c-square"), at the user’s choice of square size, is assigned a unique identifier or c-squares code, which can then be attached to any data or information that occurs within that square and used for simple geographic information retrieval or cross-matching to other systems. Visualisations of a dataset or other information’s spatial extent or "footprint" can also be generated by rendering the boundaries of its associated square or squares on an appropriate base map.
C-squares takes as its starting point the ten degree global grid square notation referred to as WMO or World Meteorological Organization squares, as illustrated by the U.S. NODC (National Oceanographic Data Center), 1998 (ref. 1; a representative portion is reproduced in Figure 1). C-squares utilises this (four digit) notation for its 10×10 degree square size. Since the c-squares notation is fully hierarchical, all smaller resolution c-squares retain these initial four digits which serve to indicate the ten degree global grid square within which they are located. C-squares also thereby incorporates the "global quadrant" notation of WMO squares, where the initial digit 1, 3, 5 or 7 indicates the global quadrant NE, SE, SW and NW, respectively (Figure 2). C-squares notation for 5×5 and 1×1 squares is also compatible with the (Australian) "Blue Pages" metadata directory’s notation for these cell sizes as subdivisions of WMO squares (ref. 2). WMO squares in global quadrant 1 are numbered 1000 through 1817, in global quadrant 3 are numbered 3000 through 3817, etc., although in each quadrant the number of values totals 162 (=9×18, covering an area 90×180 degrees), so not all possible values are used (for example, in global quadrant 1, legal values are 1000 through 1017, 1100 through 1117, 1200 through 1217, up to 1800 through 1817).

Figure 1. Portion of the Globe around the global origin (0 latitude, 0 longitude) with grid lines at 10 degree intervals, numbered according to WMO square (=c-squares 10 degree square) notation.
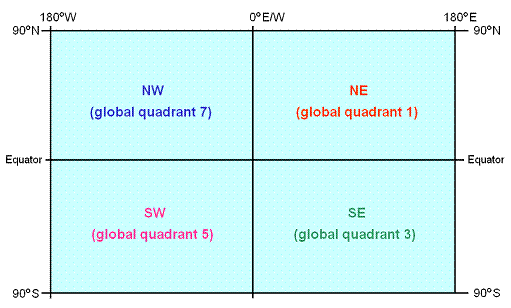
Figure 2. Identifiers for global quadrants as used in c-squares (ported from equivalent nomenclature for WMO 10 degree squares).
Individual c-squares take their nomenclature from the position of their two "minimum absolute" boundaries closest to the global origin (0 latitude, 0 longitude) in decimal degrees, with latitude preceding longitude. In other words, in the north-east global quadrant these will be the southern and the western boundary; in the south-east global quadrant these are the northern and the western boundary; in the south-west global quadrant the northern and the eastern boundary; and in the north-west global quadrant the southern and the eastern boundary. An alternative way to express this is as the minimum absolute values of latitude and longitude, i.e. 10 in the case of a cell extending from +10 to +20 degrees, -10 in the case of a cell extending from -10 to -20 degrees.
Values representing the position of these "minimum" boundaries of latitude and longitude are then encoded within a succession of one or more "cycles", where the first cycle is four digits and comprises the (WMO squares notation) 10°×10° square identifier, and successive cycles (where present) are three digits long or (in the terminal case), optionally a single digit (an incomplete cycle). Successive cycles are separated by a colon character, thus:
10 degree square code: 7307 (1 cycle, 4 characters)
5 degree square code: 7307:4 (1+ cycles, 6 characters)
1 degree square code: 7307:487 (2 cycles, 8 characters)
0.5 degree square code: 7307:487:3 (2+ cycles, 10 characters)
0.1 degree square code: 7307:487:380 (3 cycles, 12 characters)
0.05 degree square code: 7307:487:380:1 (3+ cycles, 14 characters)
0.01 degree square code: 7307:487:380:143 (4 cycles, 16 characters)
(etc.).
Absolute values of latitude in decimal degrees (i.e., regardless of sign) are represented by the second digit in every cycle, i.e. in the example above by the digits 3, 8, 8 and 4 which correspond to tens, units, tenths, and hundredths of decimal degrees (extensible as required), i.e. the value 38.84. Absolute values of longitude in decimal degrees are represented by the third and fourth digits in the first cycle (representing hundreds then tens), and the third digit of successive cycles (units, tenths, hundredths, etc.). In the example above, these values are 0, 7 (or 07), then 7, 0, 3, i.e. the value 77.03 decimal degrees. Note, the provision for an extra digit for hundreds of longitude is required because these values can go up to 180, whereas for latitude the limit is 90.
The remaining digits of the code (i.e., the leading digit in each cycle) represent the global quadrant (in cycle 1) and intermediate quadrants (in all other cycles). Global quadrants are designated as per the WMO square notation described above, e.g., the example shown above is in global quadrant 7, i.e. latitudes are positive (north), longitudes are negative (west). Intermediate quadrants are designated as described in the next section.
The digit for intermediate quadrant (1, 2, 3 or 4) is assigned according to whether the following digits for latitude and longitude in the same cycle are "low" (i.e., 0-4) or "high" (5-9), on the 0-10 scale employed. If the digits for both latitude and longitude are both low, the intermediate quadrant is 1. If latitude is low but longitude high, the value is 2. If the reverse is true (latitude high, longitude low), the value is 3. If both values are high, the intermediate quadrant is 4. In practical terms, this means that the arrangement of these intermediate quadrants varies according to global quadrant, with intermediate quadrant 1 always closest to the global origin, and intermediate quadrant 4 always furthest away (Figure 3).
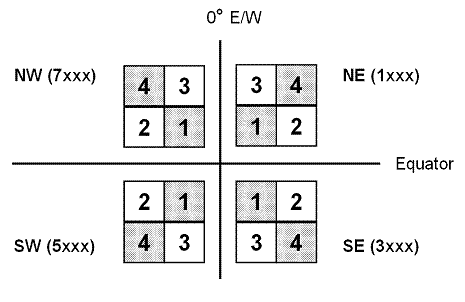
Figure 3. Identifiers for intermediate quadrants as used in c-squares. Note, arrangement varies according to global quadrant, with intermediate quadrant 1 always closest to the global origin (0,0), and intermediate quadrant 4 always furthest away.
Cells identifiers in any three digit cycle are a combination of the intermediate quadrant digit followed by the relevant single digits for latitude then longitude, representing distance away from the global origin for the "minimum" boundary at the particular scale step represented (i.e. units, tenths, hundredths of degrees, etc.). They thus fall within the range 100 to 499, and conform to the following legal values:
(intermediate quadrant 1:)
100 through 104, 110 through 114, 120 through 124, 130 through 134, 140 through 144
(intermediate quadrant 2:)
205 through 209, 215 through 219, 225 through 229, 235 through 239, 245 through 249
(intermediate quadrant 3:)
350 through 354, 360 through 364, 370 through 374, 380 through 384, 390 through 394
(intermediate quadrant 4:)
455 through 459, 465 through 469, 475 through 479, 485 through 489, 495 through 499.
The arrangement of these sub-squares varies according to the global quadrant, being mirror images across the 0 degree latitude and longitude divisions. An example arrangement in the north-west global quadrant (global quadrant 7) is shown in Figure 4.
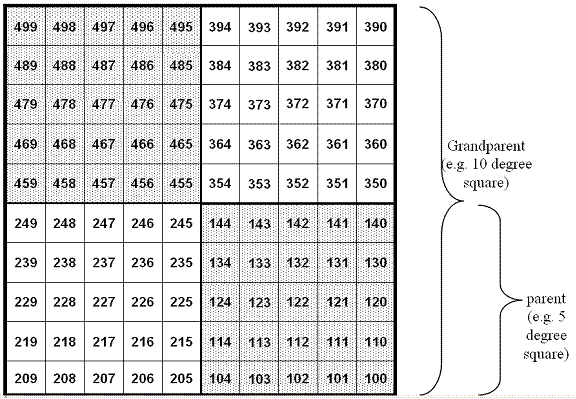
Figure 4. Arrangement of identifiers for (e.g.) 1 degree squares within ‘parent’ 5 degree squares (intermediate quadrants) and ‘grandparent’ 10 degree squares, in one of the four global quadrants (north-west in this case, compare Figure 3). Note, each square identifier comprises a pair of digits 00 through 99, prefixed by the relevant intermediate quadrant identifier; thus the sequence spans 100 through 499, and only a subset of these 400 potential combinations are valid.
A c-squares string is defined as a set of one or more valid c-squares codes at the same resolution, each separated by the vertical bar or "pipe" character (|). For example, 1000:1|1000:2|1000:3|1000:4 . No other characters are permitted in a c-squares string with the exception of the wildcard (asterisk) character (see below). A c-squares string may not start, or end with, the vertical bar character.
To reduce the number of codes that may be required to be expressed in a c-squares string, a "compressed" notation (previously also cited as "compacted" notation) is available whereby if all squares at one or more subsidiary levels are to be designated within a single higher level "parent" cell, the relevant number of asterisk characters can be inserted to indicate that all possible values are encompassed. For example:
1000:* can be used in place of the four possible values 1000:1 through 1000:4
1000:*** can be used in place of the one hundred possible values 1000:100 through 1000:499
1000:1** can be used in place of the twenty five possible values 1000:100 through 1000:144
1000:***:* can be used in place of the four hundred possible values 1000:100:1 through 1000:499:4
etc. The digits in place before any asterisk must themselves denote a valid c-squares code at the higher level. Colon separator characters are retained at the equivalent places within the asterisk string as if the latter were true digits. No numeric characters can follow an asterisk once used (within a single "compressed" code), and (as for numeric characters), cycles comprising all or part asterisks must either be complete (three characters) or (optionally, for the terminal cycle only) incomplete (1 character).
For c-squares, latitude and longitude are expressed with reference to the World Geodetic System 1984 (WGS84) Datum.
Points are allocated to the square in which they reside, at the user’s choice of resolution (refer Section 11 below for usage guidelines). For treatment of zero values and "on the line" cases, see below. Lines and areas are allocated to the square or squares which they intersect, either completely or partially. If desired, a particular user or system may choose to distinguish between squares which are completely occupied by data areas and those which are only partly occupied, for use in subsequent spatial queries.
Zero is considered to be positive (i.e., a point at 0 latitude, 0 longitude encodes within the north-east global quadrant)
Points "on the line" are normally encoded within the next "higher" square, i.e. further away from the global origin (for exceptions, refer 9.3 below). In other words, a point at +10 latitude will be encoded within the ten degree square covering +10 to +20, not 0 to +10; a point at -10 latitude will be encoded within the ten degree square covering -10 to -20, not 0 to -10.
Exceptions to this rule are as follows:
The length of a degree of latitude is approximately constant, at around 111 kilometers. The length of a degree of longitude varies according to its distance from the equator, being approximately 111 kilometers at the equator, 96 kilometers at latitude 30 degrees (north or south), 56 kilometers at latitude 60 degrees (north or south), and zero at the poles (ref. 3). The size of an area represented by an individual c-square will vary accordingly, e.g. for a one degree square, between approximately 12,300 km2 adjacent to the equator to approximately 109 km2 adjacent to the poles. Additional values computed for all possible c-squares for a range of sizes (10, 5, 1 and 0.5 degree squares) are available from the c-squares web site, http://www.cmar.csiro.au/csquares/.
A suggested "minimum" resolution (square size) for potential global interoperability of data or other information systems is 1 degree squares (around 100 km nominal resolution or better), although a number of global projects including LOICZ, the Sea Around Us Project, OBIS, and AquaMaps have adopted 0.5 degree squares (50 km nominal) as their basic operating unit on account of its increased resolution particularly around complex shapes such as coastlines, etc. (It should be noted that information encoded at, for example, 0.5 degree resolution can always be queried at a coarser scale, e.g. 1 degree squares, but the reverse is not true). For more local usage, 0.1 degree squares (10 km nominal), or finer resolutions (0.05 or 0.01 degree squares, 5 km or 1 km nominal) may also be appropriate.
Additional information regarding the c-squares system is available at the c-squares web site, http://www.cmar.csiro.au/csquares/, and in refs. 4 and 5, below.
[1] National Oceanographic Data Center (NODC), 1998. World Ocean Database 1998: Documentation and Quality Control, Version 1.2 (National Oceanographic Data Center Internal Report 14). (Silver Spring, MD: Ocean Climate Laboratory, National Oceanographic Data Center). Appendices 10A and 10B (WMO squares for Atlantic/Indian and Pacific Oceans) available online at: http://www.nodc.noaa.gov/OC5/wmoatlind.html and http://www.nodc.noaa.gov/OC5/wmopacific.html.
[2] Australian Oceanographic Data Centre / Environmental Resources Information Network (AODC/ERIN), 1996. The Marine and Coastal Data Directory of Australia - The Blue Pages.
[3] National Imagery and Mapping Agency (NIMA). Length of a Degree of Latitude and Longitude. Available online at: http://pollux.nss.nima.mil/calc/degree.html.
[4] Rees, Tony, 2003. "C-squares", a new spatial indexing system and its applicability to the description of oceanographic datasets. Oceanography, vol. 16(1): 11-19. Available online at: http://www.cmar.csiro.au/csquares/csq-article-Mar03-lowres.pdf.
[5] Rees, Tony, 2006. The c-squares manual: principles and practice of the concise spatial query and representation system. CSIRO Marine and Atmospheric Research Paper (in prep.)
This page last updated 13 December 2005.
File location: http://www.cmar.csiro.au/csquares/spec1-1.htm